Present and future value of money

THE FUTURE VALUE OF MONEY

Anyone can invest his own money on the market to earn interest and, because of that earning possibility, having a dollar now is better than having a dollar in the future. When you decide to invest, you give up the possibility to spend the money you have now to spend more in the future. If you continue to invest also the money you earn your wealth will grow at a compound rate and, thanks to that, you achieve a compound interest. The expression future value (FV) indicates how much money you will have in the future if you invest a certain amount C for a number of periods t (generally years) at an interest rate r. The formula to calculate this future value is:

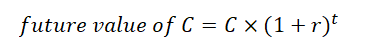
THE PRESENT VALUE OF MONEY

If instead, you want to ask yourself how much money you have to invest today to have a certain amount C in the future you are asking yourself what is the present value of C. The present value of C is computed as follows:

The r in that formula indicates the discount rate while 1/(1+r)^t indicates the discount factor and it simply measures the present value of 1 dollar the you will receive in period t.

THE NET PRESENT VALUE OF AN INVESTMENT

When deciding whether an investment is worth or not, you need to consider its net present value (NPV). It is simply computed as the present value of the investment minus the cost required to conduct it:

In the formula C0 represents the cashflow at period 0 (the present) and generally is a negative number while Ct represents the cashflow received in period t. When considering an investment you should also take into account its riskiness: if you are like most investors, you do not like taking risks with your money. In order to accept risks you have to get higher sums of money in return.

WHAT IF AN INVESTMENT WILL GENERATE MULTIPLE CASHFLOWS IN THE FUTURE

If you are considering an investment that will produce multiple cashflows in the future, you can still calculate its present value with the discounted cash flow (DCF) formula by summing the present values of its cashflows over the years:

Or

In this case the Net present value is computed as:

WHAT IS A PERPRETUITY AND HOW TO VALUE IT

A perpetuity is a bond that enables who buys it to receive for ever a fixed amount of money C each period. The value of a perpetuity is computed as the fixed cashflow received per period divided by the discount rate r:

If the perpetuity you want to buy does not start giving you money for some years you can still calculate its value by slightly modifying the formula:

In that formula t indicates the number of years during which the perpetuity does not pay any money. So if for example you will start receiving money at period 5 you will use t=4.

WHAT IS AN ANNUITY AND HOW TO VALUE IT

An annuity gives the buyer the right to receive a fixed amount of money C each period but for a limited number of periods t. The present value of an annuity is computed as:

The term written in the square brackets is called the t-year annuity factor and it indicates the present value of $1 paid for each of the t years the annuity offers its revenues. If once you buy an annuity you receive immediately a payment you are then considering a special kind of annuity called annuity due and it is worth (1+r) times the present value of a normal annuity. If you want to compute the future value of an annuity in period t you can compute it by multiplying the present value of that annuity for (1+r)^t:

WHAT IF A PERPETUITY OR AN ANNUITY GROWS EACH YEAR

If the amount received thanks to an annuity or a perpetuity grows each period by a certain percentage g and if we assume that the discount rate r is greater than g you can calculate still calculate their present values:

DIFFERENT KINDS OF INTEREST

When talking about interest rate it is important to distinguish between quoted interest rates and effective interest rates. The quoted interest rate is computed as the total payment that should be received at the end of the year divided by the number of payments (m) while the effective interest rate is computed as:

This means that, if you receive money only once a year, the quoted interest rate and the effective interest rate are the same while if you receive your interest multiple times during the year the quoted interest rate will be lower than the effective interest rate. If you get your interests constantly meaning that you divide the year in infinite parts, what will happen to your interest rate? To answer this question a bit of limit theory is needed: you can solve this by noticing that the first part of the formula is a special limit. As m approaches infinity it becomes e^r which is (2.718)^r. If you receive an annual interest of r constantly during a year for t numbers of years, your interest rate will become in the end: e^(rt) so (2.718)^rt.